Mathematik
Zur Navigation springen
Zur Suche springen
| Einzelheit Monadisches Paradigma Zahl |
Konstellation Relationales Paradigma Beziehung (als spaltbares Verhältnis) |
Situation Topisches Paradigma Unspaltbares Verhältnis | |
|---|---|---|---|
| Mathematik | alte Mathematik | neue Mathematik (seit Hilbert/Bourbaki) | (nicht beachtet) |
| Anthropologie | alte Anthropologie | neue (Buber, Mead), relationale systemische Sicht | neue topische Sicht |
| Familientherapie | Individualtherapie (Freud etc.) | Strukturelle Familientherapie (SFT) des Systems | Leiblich, Kontextuelles Geschehen (Hypnosystemisch) |
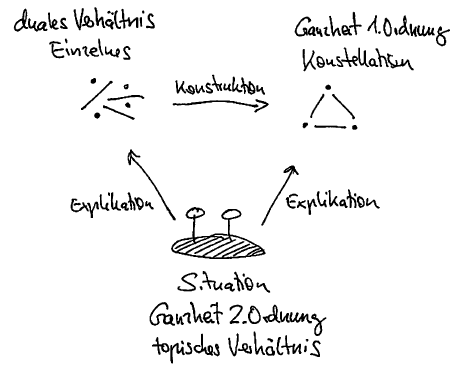 Siehe: Einzelheit, Konstellation, Situation
Siehe: Einzelheit, Konstellation, Situation
Seit Hilbert und anderen, endgültig seit der Arbeit des französischen Mathematikzirkels Bourbaki, ist die Mathematik einer durchgreifenden Formalisierung unterworfen, die darin besteht, dass nicht mehr über bestimmte Gegenstände gesprochen wird, sondern über Systeme von Beziehungen zwischen unbestimmt gelassenen Gegenständen, für die es zwar noch eine primär intendierte, bevorzugte Deutung gibt, aber auch andere Deutungen zugelassen werden. Die Beziehung hat als primäres Thema der Mathematik die Zahl eingeholt oder gar überholt. Dagegen sind die Mathematiker blind für die Verhältnisse geblieben, die den Beziehungen zu Grunde liegen, aus denen sie hervorgehen. Das hängt mit der Option für das numerische Mannigfaltige zusammen. Es scheint geboten, den Horizont der Mathematik zu erweitern, indem hinter den Beziehungen die Verhältnisse aufgedeckt und zu den aus ihnen hervorgehenden Beziehungen ins Verhältnis gesetzt werden. (S-KGM 97)
Die Mathematik ist gleichsam die Avantgarde des Versuchs, sich in einer autonom gewordenen Welt des bloß noch numerischen Mannigfaltigen mit Beziehungen zwischen Elementen von Mengen einzurichten. Sie ignoriert die Genealogie der Einzelheit, das chaotische Mannigfaltige und den Zwiespalt; durch Fehldeutung der Existenz als partikuläre Quantifikation ("Existenzquantor", "Seinszeichen") verleugnet sie den Fluss der Zeit, in dem das Seiende nur eine schmale Schwelle zwischen Nichtseinendem ist, und ebnet den Gegensatz von Seiendem und Nichtseiendem ein, damit den Spielraum, den der Mensch zum Überholen der vorgegebenen Situation benötigt. (S-KGM 107f)
Die Mathematik ist die Kunst, alle erdenklichen Kombinationen von Einzelnem mit Abschälung des Stoffes und Reduktion auf die formale Struktur auszuprobieren und in die Konsequenzen zu verfolgen. Sie ist damit die Avantgarde des spezifisch menschlichen Bestrebens, das Gegebene durch Zusammensetzung von Einzelnem zu rekonstruieren und zu überholen. Diese Übereinstimmung in der Tendenz führt dazu, dass die Menschen gerade das sehen wollen, was die Mathematik ihnen zeigt, und sich über die Übereinstimmung mit der Realität freuen und wundern, ohne zu bedenken dass sie das Ergebnis eines Ausleseprozesses ist, bei dem die Mathematik ihnen vorleuchtet.Ein Ausleseprozess gehört dazu, weil die Menschen sich nicht vollständig und ausschließlich in den Zaubergarten des numerischen Mannigfaltigen versetzen können, sondern dafür von Mannigfaltigem zehren müssen, das nicht numerisch ist: von Situationen, darunter vielsagenden Eindrücken, mit binnendiffuser Bedeutsamkeit, vom Kontinuum, von dem spältigen Mannigaltigen, das auch sie selbst sind, von Atmosphären des Gefühls, von der leiblichen Dynamik und leiblichen Kommunikation. Von all diesem Mannigfaltigem, zu dem die Mathematik keinen Zugang hat, wenden sie sich ab zur Domäne der Mathematik, zur numerischen Mannigfaltigkeit mit lauter einzelnen Inhalten. Dann ist es kein Wunder, dass sie eine Übereinstimmung dieser Realität mit den Ergebnissen der Mathematik feststellen. (S-KGM 147f)
Siehe: Relationales Paradigma
Mathematik und Topologie
Topologisches Denken im weiteren Sinn ist mit dem mathematischen also oft nur lose und indirekt verbunden. Einer der Gründe, weshalb von einer strikten ‘Anwendung’ mathematischer Konzepte nur in Ausnahmefällen gesprochen werden kann, wurde bereits erwähnt: Die mathematische Disziplin namens Topologie ist aus der Mathematisierung eines älteren Wissens - eines Knoten-Wissens und Labyrinth-Wissens etwa - hervorgegangen, das seinerseits in Alltagspraktiken, Spielen und Kunstwerken fort- oder nachlebt. (Pichler 22)